3ος Πανελλήνιος Γραπτός ΑΣΕΠ - Αναλύοντας έναν άλλο τύπο αριθμητικού συλλογισμού

Σύμφωνα με τον Πρόεδρο του ΑΣΕΠ, ο 3ος Πανελλήνιος Γραπτός Διαγωνισμός θα διεξαχθεί κανονικά, όπως έχει προγραμματιστεί, και αναμένεται να προκηρυχθεί λίγο πριν από τη λήξη του 2027.
Το περιεχόμενο της εξέτασης, τόσο ως προς τις γνώσεις όσο και ως προς τις δεξιότητες, θα γίνει γνωστό τη στιγμή της επίσημης δημοσίευσης της προκήρυξης. Μέχρι τότε, μέσα από τις δημοσιεύσεις μου για τον ΑΣΕΠ, θα εστιάσω στην προετοιμασία σας για οποιαδήποτε ενδεχόμενη ερώτηση σχετίζεται με δεξιότητες.
Όσον αφορά τις γνώσεις, το πιο πιθανό είναι, όπως συνέβη και στον 2ο Πανελλήνιο Γραπτό Διαγωνισμό (1Γ/2025), να δοθεί εκ των προτέρων τράπεζα θεμάτων, από την οποία θα αντληθούν αυτούσια κάποια από τα εξεταζόμενα ερωτήματα. Επομένως, σε αυτή τη φάση, η ουσιαστική προετοιμασία εστιάζεται στις δεξιότητες.
Σήμερα θα ασχοληθούμε με τους αριθμητικούς συλλογισμούς. Όχι, με αυτούς που τέθηκαν στον 1ο Πανελλήνιο Γραπτό Διαγωνισμό του ΑΣΕΠ (2Γ/2022), αλλά με ένα άλλο τύπο αριθμητικών συλλογισμών που χρησιμοποιείται ευρέως από μεγάλους οργανισμούς του εξωτερικού που αξιολογούν υποψηφίους για τις εταιρείες πελάτες τους. Ακόμη και η Ευρωπαϊκή Υπηρεσία Επιλογής Προσωπικού βασίζεται σε αυτό το είδος.
Φυσικά, τα θέματα που θα συναντήσετε στον διαγωνισμό δεν θα είναι ίδια με αυτά που θα δούμε μαζί στα δύο επόμενα χρόνια αλλά πανομοιότυπα. Το ΑΣΕΠ όπως ήδη γνωρίζουμε δεν δημοσιοποιεί πλέον τα θέματα που θέτει σε κάθε γραπτό πανελλήνιο διαγωνισμό, αυτό συνέβη μόνο στον 1ο Πανελλήνιο Γραπτό Διαγωνισμό. Ωστόσο, μελετώντας παρόμοια παραδείγματα, μπορείτε να αποκτήσετε εξοικείωση με τον τρόπο σκέψης που απαιτείται και να γνωρίζετε τι να περιμένετε.
Οι αριθμητικοί συλλογισμοί αποτελούν έναν από τους βασικούς άξονες δεξιοτήτων που αξιολογούνται σε διαγωνισμούς επιλογής προσωπικού, είτε πρόκειται για τον ΑΣΕΠ είτε για την Ευρωπαϊκή Υπηρεσία Επιλογής Προσωπικού.
Δεν εξετάζουν απλώς την ικανότητα υπολογισμών, αλλά κυρίως τη λογική επεξεργασία αριθμητικών δεδομένων, την ταχύτητα εξαγωγής συμπερασμάτων και την ικανότητα λήψης αποφάσεων με βάση αριθμητικά στοιχεία. Οι υποψήφιοι καλούνται να κατανοήσουν πίνακες, διαγράμματα, ποσοτικά δεδομένα και αριθμητικές σχέσεις, ώστε να απαντούν με ακρίβεια και σε σύντομο χρόνο.
Αυτό που πρέπει να γνωρίζουν οι υποψήφιοι είναι ότι τα ερωτήματα αυτής της κατηγορίας δεν απαιτούν υψηλό επίπεδο θεωρητικών μαθηματικών γνώσεων, αλλά μια καλή κατανόηση βασικών αριθμητικών εννοιών. Η επιτυχία σε αυτού του είδους τις ερωτήσεις εξαρτάται κυρίως από την ικανότητα ερμηνείας δεδομένων, την προσοχή στη λεπτομέρεια και την ορθολογική προσέγγιση της επίλυσης.
Από πλευράς αριθμητικής, οι υποψήφιοι θα πρέπει να έχουν εξοικειωθεί με:
- Βασικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό, διαίρεση)
- Ποσοστά (υπολογισμός ποσοστών αύξησης ή μείωσης, καθώς και αντίστροφα ποσοστά, όπου πρέπει να βρείτε να βρείτε την αρχική τιμή)
- Αναλογίες (κατανόηση των σχέσεων μεταξύ αριθμών και δεδομένων)
- Μέσο όρο (υπολογισμός απλών και σταθμισμένων μέσων όρων)
- Διαχείριση μονάδων (π.χ. ευρώ, ώρες, κιλά)
- Υπολογισμοί με ρυθμούς (προβλήματα που σχετίζονται με απόσταση/ταχύτητα /χρόνο)
- Διάκριση απόλυτων και σχετικών τιμών (κατανόηση της διαφοράς μεταξύ των πραγματικών αριθμών και των σχετικών τιμών που δίνονται σε ποσοστά ή αναλογίες)
Η καλύτερη προετοιμασία έγκειται στη συστηματική εξάσκηση με πρακτικά παραδείγματα, την ανάλυση λαθών και την εξοικείωση με χρονικούς περιορισμούς. Όσο περισσότερο εξασκούνται οι υποψήφιοι σε αυτό το είδος προβλημάτων, τόσο αυξάνουν την ταχύτητα και την ακρίβειά τους.
Παρακάτω ακολουθούν δέκα ερωτήματα αριθμητικών συλλογισμών προς επίλυση:
Ερώτημα 1ο
Ένας πελάτης έχει ένα χαρτοφυλάκιο με μετοχές σε 5 εταιρείες και εξετάζει την ετήσια απόδοσή τους:
Μεταξύ 1ης Ιανουαρίου και 1ης Μαΐου, η τιμή της μετοχής της Λιανικής πέφτει κατά 10%. Ποιο είναι το ποσοστό αύξησης της τιμής ανά μετοχή μεταξύ της 1ης Μαΐου και 31ης Δεκεμβρίου;
Α. 28,78%
Β. 22,35%
Γ. 27,73%
Δ. 18,60%
Ε. 25,91%
Επίλυση ερωτήματος 1ου:
Βήμα 1ο: Υπολογισμός της τιμής της μετοχής την 1η Μαίου μετά από πτώση 10%: Η αρχική τιμή της μετοχής Λιανικής την 1η Ιανουαρίου είναι 440 ευρώ. Πτώση 10% σημαίνει:
440 Χ (1 – 0,10) = 396
Άρα, η τιμή της μετοχής την 1η Μαΐου είναι 396 ευρώ.
Βήμα 2ο: Υπολογισμός ποσοστού αύξησης από 1η Μαΐου έως 31η Δεκεμβρίου: Το ποσοστό μεταβολής υπολογίζεται ως το πηλίκο της διαφοράς τελικής και αρχικής τιμής προς την αρχική τιμή, πολλαπλασιασμένο επί 100 για να εκφραστεί σε ποσοστό. Οπότε, η τελική τιμή της μετοχής στις 31 Δεκεμβρίου είναι 510 ευρώ. Υπολογίζουμε το ποσοστό αύξησης από τα 396 ευρώ:
(510-396)/396 Χ 100 ≈ 28,78%
Ερώτημα 2ο
Ένας πελάτης έχει ένα χαρτοφυλάκιο με μετοχές σε 5 εταιρείες και εξετάζει την ετήσια απόδοσή τους:
Ποιος από τους παρακάτω λόγους αντιπροσωπεύει καλύτερα την αναλογία του αριθμού των μετοχών που κατείχε η Λιανική και η Ενέργεια την 1η Ιανουαρίου;
Α. 2:3
Β. 9:13
Γ. 9:14
Δ. 10:7
Ε. 3:2
Επίλυση ερωτήματος 2ου:
Βήμα 1ο: Καθορισμός του αριθμού των μετοχών για τα δύο είδη εταιρειών: Λιανική: 9.000 μετοχές και Ενέργεια: 13.500 μετοχές.
Βήμα 2ο: Υπολογισμός της αναλογίας: Θέλουμε την αναλογία 9.000:13.500.
Βήμα 3ο: Απλοποίηση της αναλογίας: Για να απλοποιήσουμε μια αναλογία, διαιρούμε και τα δύο μέρη της με τον μέγιστο κοινό διαιρέτη τους. Αυτό μας δίνει την αναλογία στη μικρότερη δυνατή μορφή της, χωρίς να αλλάζει η σχέση μεταξύ των ποσοτήτων. Οπότε, βρίσκουμε το μέγιστο κοινό διαιρέτη (ΜΚΔ), ο οποίος είναι:
13.500/9.000 = το 9.000 χωράει στο 13.500 μία φορά και το υπόλοιπο που έμεινε είναι 4.500, οπότε συνεχίζουμε,
9.000/4.500 = το 4.500 χωράει στο 9.000 δύο φορές και μας μένει 0 οπότε ο προηγούμενος διαιρέτης είναι ο ΜΚΔ δηλαδή ΜΚΔ (9.000, 13.500) = 4.500.
Έτσι, 9.000:13.500 = (9.000/4.500) : (13.500/4.500) = 2:3
Ερώτημα 3ο
Ένας πελάτης έχει ένα χαρτοφυλάκιο με μετοχές σε 5 εταιρείες και εξετάζει την ετήσια απόδοσή τους:
Σε μία περίοδο 3 ετών, η τιμή ανά μετοχή του είδους εταιρείας Αναψυχή αναμένεται να παρουσιάσει την ίδια ετήσια ποσοστιαία μεταβολή όπως και το πρώτο έτος. Ποια είναι η αναμενόμενη τιμή ανά μετοχή της Αναψυχής στο τέλος της τριετούς περιόδου;
Α. 307 ευρώ
Β. 310 ευρώ
Γ. 337 ευρώ
Δ. 361 ευρώ
Ε. 408 ευρώ
Επίλυση ερωτήματος 3ου:
Βήμα 1ο: Υπολογισμός της ετήσιας ποσοστιαίας μεταβολής της μετοχής Αναψυχής: Τιμή 1ης Ιανουαρίου: 190 ευρώ, Τιμή 31ης Δεκεμβρίου: 230 ευρώ:
Ετήσιος συντελεστής μεταβολής = 230/190 ≈ 1,2105
Βήμα 2ο: Εφαρμογή της ίδιας ετήσιας μεταβολής για 3 έτη (ανατοκισμός): Όταν μια ποσότητα αυξάνεται κάθε χρόνο με το ίδιο ποσοστό, η αύξηση δεν είναι απλή αλλά ανατοκιζόμενη. Δηλαδή η αύξηση κάθε χρόνου εφαρμόζεται πάνω στη νέα αυξημένη τιμή, οπότε η τιμή μετά από 3 έτη θα είναι:
190 Χ (1,2105)3 ≈ 337,04 ευρώ
Ερώτημα 4ο
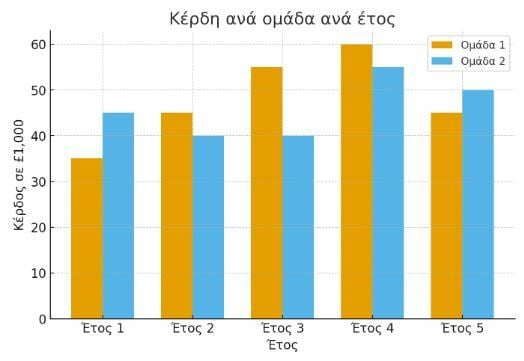
Αυτό το διάγραμμα δείχνει τα ετήσια κέρδη δύο ομάδων μιας εταιρείας σε διάστημα 5 ετών:
Κατά τη διάρκεια της περιόδου από το Έτος 1 έως και το Έτος 4, ποιο είναι το συνολικό κέρδος της Ομάδας 1;
Α. 240.000 λίρες
Β. 183.000 λίρες
Γ. 135.000 λίρες
Δ. 195.000 λίρες
Ε. 180.000 λίρες
Απάντηση ερωτήματος 4ου:
Βήμα 1ο: Ανάγνωση των κερδών της Ομάδας 1 από το ραβδόγραμμα: Τα ετήσια κέρδη (σε χιλιάδες λίρες) για την Ομάδα 1 είναι:
Έτος 1: 35.000 λίρες
Έτος 2: 45.000 λίρες
Έτος 3: 55.000 λίρες
Έτος 4: 60.000 λίρες
Βήμα 2ο: Υπολογισμός του συνολικού κέρδους για τα 4 έτη: Για να βρεις το συνολικό κέρδος από ραβδόγραμμα, παρατηρείς το ύψος κάθε ράβδου που αντιστοιχεί στις χρονιές που σε ενδιαφέρουν και αθροίζεις τις τιμές τους. Είναι σημαντικό να διαβάζεις σωστά τη μονάδα μέτρησης του διαγράμματος (εδώ είναι σε χιλιάδες λίρες) και να μετατρέπεις αναλόγως: 35 + 45 + 55 + 60 = 195 (χιλιάδες λίρες) = 195.000 λίρες.
Ερώτημα 5ο
Αυτό το διάγραμμα δείχνει τα ετήσια κέρδη δύο ομάδων μιας εταιρείας σε διάστημα 5 ετών:
Ποια είναι η μεγαλύτερη διαφορά μεταξύ των κερδών που πραγματοποίησαν οι δύο ομάδες σε ένα έτος;
Α. 5.000 λίρες
Β. 10.000 λίρες
Γ. 15.000 λίρες
Δ. 20.000 λίρες
Ε. 25.000 λίρες
Επίλυση ερωτήματος 5ου:
Βήμα 1ο: Καταγραφή των ετήσιων κερδών και υπολογισμός των διαφορών: Από το διάγραμμα έχουμε τα ετήσια κέρδη (σε χιλιάδες λίρες) για κάθε ομάδα ως εξής:
Έτος 1: Ομάδα 1 – Ομάδα 2 = 35-45=10
Έτος 2: Ομάδα 1 – Ομάδα 2 = 45-40=5
Έτος 3: Ομάδα 1 – Ομάδα 2 = 55-40=15
Έτος 4: Ομάδα 1 – Ομάδα 2 = 60-55=5
Έτος 5: Ομάδα 1 – Ομάδα 2 = 45-50=5
Βήμα 2ο: Εύρεση της μέγιστης διαφοράς: Η μεγαλύτερη διαφορά εμφανίζεται στο Έτος 3 όπου: 55-40=15 χιλιάδες λίρες = 15.000 λίρες.
Ερώτημα 6ο
Αυτό το διάγραμμα δείχνει τα ετήσια κέρδη δύο ομάδων μιας εταιρείας σε διάστημα 5 ετών:
Ποιο είναι το μέσο ετήσιο κέρδος της Ομάδας 2 για την περίοδο των 5 ετών;
Α. 46.000 λίρες
Β. 48.000 λίρες
Γ. 50.000 λίρες
Δ. 230.000 λίρες
Ε. 240.000 λίρες
Επίλυση ερωτήματος 6ου:
Βήμα 1ο: Καταγραφή των κερδών της Ομάδας 2 για κάθε έτος: Από το διάγραμμα (γαλάζιες μπάρες για Ομάδα 2), τα ετήσια κέρδη (σε χιλιάδες λίρες) είναι:
Έτος 1: 45, Έτος 2: 40, Έτος 3: 40, Έτος 4: 55, Έτος 5: 50
Βήμα 2ο: Υπολογισμός του συνολικού κέρδους: 45+40+40+55+50=230 χιλιάδες λίρες.
Βήμα 3ο: Υπολογισμός του μέσου ετήσιου κέρδους: Ο αριθμητικός μέσος όρος υπολογίζεται προσθέτοντας όλες τις τιμές και διαιρώντας το άθροισμα με το πλήθος των τιμών. Είναι ένα μέτρο κεντρικής τάσης που χρησιμοποιείται για να εκτιμήσουμε την «τυπική» τιμή ενός συνόλου δεδομένων. Ειδικότερα:
230/5 = 46 χιλιάδες λίρες = 46.000 λίρες.
Ερώτημα 7ο
Αυτό το διάγραμμα δείχνει τα ετήσια κέρδη δύο ομάδων μιας εταιρείας σε διάστημα 5 ετών:
Ποιος από τους παρακάτω λόγους αντιπροσωπεύει καλύτερα την αναλογία των κερδών μεταξύ της Ομάδας 1 στο Έτος 2 και της Ομάδας 2 στο Έτος 4;
Α. 1:2
Β. 2:3
Γ. 3:4
Δ. 8:11
Ε. 9:11
Επίλυση ερωτήματος 7ου:
Βήμα 1ο: Εντοπισμός των ζητούμενων τιμών από το διάγραμμα: Ομάδα 1 στο Έτος 2: 45 (χιλιάδες λίρες), Ομάδα 2 στο Έτος 4: 55 (χιλιάδες λίρες).
Βήμα 2ο: Υπολογισμός του λόγου κερδών: Η αναλογία εκφράζει τη σχετική σχέση μεγέθους μεταξύ δύο τιμών. Για να υπολογίσεις έναν λόγο, διαιρείς τις δύο ποσότητες και αν χρειαστεί, απλοποιείς το κλάσμα, όπως με τους αριθμούς 45 και 55. Οι λόγοι χρησιμοποιούνται συχνά σε συγκρίσεις ποσοτήτων. Ο λόγος Ομάδα 1 (Έτος 2) προς Ομάδα 2 (Έτος 4) είναι: 45/55
Βήμα 3ο: Εύρεση Μέγιστου Κοινού Διαιρέτη (ΜΚΔ): Πρέπει να βρούμε τον ΜΚΔ του 45 και του 55 για να απλοποιήσουμε τον λόγο: 45/55, διαιρώντας και τον αριθμητή και τον παρονομαστή και να πάρουμε τον λόγο στην πιο απλή μορφή ως εξής:
Διαιρέτες του 45: 1, 3, 5, 9, 15, 45
Διαιρέτες του 55: 1, 5, 11, 55
Ο κοινός μέγιστος διαιρέτης = 5, άρα 45:5/55:5 = 9/11.
Ερώτημα 8ο
Ο παρακάτω πίνακας δείχνει τις ώρες εργασίας πέντε υπαλλήλων για μια εβδομάδα, όποιος υπάλληλος εργάζεται πάνω από 35 ώρες πληρώνεται την κάθε παραπάνω ώρα ως «μία και μισή»:
Ποιος υπάλληλος αμείβεται με το υψηλότερο ωρομίσθιο;
Α. Άρης
Β. Βασίλης
Γ. Χρήστος
Δ. Ντίνος
Ε. Ελένη
Επίλυση ερωτήματος 8ου:
Βήμα 1ο: Υπολογισμός «πραγματικών αμειβόμενων ωρών» για κάθε υπάλληλο: Το ωρομίσθιο προκύπτει από τη διαίρεση της συνολικής μικτής αμοιβής με τις συνολικές πληρωτέες ώρες, λαμβάνοντας υπόψη τις υπερωρίες ως 1,5 φορά για κάθε ώρα πάνω από το κανονικό όριο (35 ώρες στην περίπτωση αυτή). Έτσι, το ωρομίσθιο αποτυπώνει το πραγματικό ποσό που πληρώνεται ανά ώρα εργασίας:
Άρης: 300/23 = 13,04
Βασίλης: 400/(35+2*1,5)=400/38=10,53
Χρήστος: 500/(35+5*1,5)=500/42,5=11,76
Ντίνος: 520/(35+7*1,5)=520/45,5=11,43
Ελένη: 380/33=11,52
Βήμα 2ο: Σύγκριση των ωρομισθίων: Άρης (με ωρομίσθιο 13,04).
Ερώτημα 9ο
Ο παρακάτω πίνακας δείχνει τις ώρες εργασίας πέντε υπαλλήλων για μια εβδομάδα, όποιος υπάλληλος εργάζεται πάνω από 35 ώρες πληρώνεται την κάθε παραπάνω ώρα ως «μία και μισή»:
Ποιος υπάλληλος έχει το μικρότερο ποσοστό κρατήσεων από τον ακαθάριστο μισθό του;
Α. Άρης
Β. Βασίλης
Γ. Χρήστος
Δ. Ντίνος
Ε. Ελένη
Επίλυση ερωτήματος 9ου:
Βήμα 1ο: Κατανόηση του ερωτήματος: Θέλουμε να βρούμε ποιος έχει το μικρότερο ποσοστό κρατήσεων επί της μικτής (ακαθάριστης) αμοιβής. Θα χρησιμοποιήσουμε τον τύπο:
Ποσοστό κρατήσεων = Κρατήσεις / Μικτή αμοιβή * 100
Βήμα 2ο: Υπολογισμός για κάθε υπάλληλο: Για να βρούμε το ποσοστό ενός ποσού σε σχέση με ένα άλλο, διαιρούμε το πρώτο με το δεύτερο και πολλαπλασιάζουμε επί 100. Αυτή η τεχνική χρησιμοποιείται ευρέως σε οικονομικά και στατιστικά προβλήματα για να εκφράσει αναλογίες:
Άρης: (70/300) Χ 100 = 23,33%
Βασίλης: (90/400) Χ 100 = 22,50%
Χρήστος: (110/500) Χ 100 = 22%
Ντίνος: (120/520) Χ 100 = 23,08%
Ελένη: (80/380) Χ 100 = 21,05%
Οπότε, η Ελένη είναι η απάντησή μας.
Ερώτημα 10ο
Ο παρακάτω πίνακας δείχνει τις ώρες εργασίας πέντε υπαλλήλων για μια εβδομάδα, όποιος υπάλληλος εργάζεται πάνω από 35 ώρες πληρώνεται την κάθε παραπάνω ώρα ως «μία και μισή»:
Για πόσους από τους υπαλλήλους η καθαρή αμοιβή είναι μικρότερη από το 80% της ακαθάριστης αμοιβής τους;
Α. 1
Β. 2
Γ. 3
Δ. 4
Ε. 5
Επίλυση ερωτήματος 10ου:
Βήμα 1ο: Κατανόηση του ερωτήματος: Θέλουμε να βρούμε πόσοι υπάλληλοι έχουν καθαρή αμοιβή < 80% της μικτής αμοιβής. Χρησιμοποιούμε τον τύπο:
Καθαρή αμοιβή / Μικτή αμοιβή Χ 100 < 80
Βήμα 2ο: Υπολογισμός για κάθε υπάλληλο: Για να συγκρίνουμε αν ένα ποσό είναι κάτω από κάποιο ποσοστό ενός άλλου, διαιρούμε το μικρότερο με το μεγαλύτερο και συγκρίνουμε το αποτέλεσμα με την αντίστοιχη τιμή σε ποσοστό (εδώ 80%). Αυτή η τεχνική είναι χρήσιμη για ελέγχους κόστους, αποδοτικότητας ή κρατήσεων. Ειδικότερα:
Άρης: 230/300 Χ 100 = 76,67%
Βασίλης: 310/400 Χ 100 = 77,5%
Χρήστος: 390/500 Χ 100 = 78%
Ντίνος: 400/520 Χ 100 = 76,92%
Ελένη: 300/380 Χ 100 = 78,95%
Επομένως, όλοι οι υπάλληλοι έχουν καθαρή αμοιβή μικρότερη από το 80% της μικτής.